In traditional literature, transformational harmony is considered non-functional (Cohn 1996). Here, a new framework is presented to view transformational progressions with tensional areas, called levels, that parallel the system of tension and release seen in functional harmony. These levels section off phrases into areas of varying levels of tension and lack of tension. Neo-Riemannian transformations, simplified into common tone relations between triads dictate how and what level the phrase begins on, and then moves towards. Further application of this theory divides arias into subsections based on tension and release. Examples from “News has a kind of mystery” from John Adams’s Nixon in China are used to showcase this novel theory.
There are three transformations. All three transformations take a triad and change a note in the triad to alter the quality, root note, or both.
- Basic transformations are used when two triads share two common tones.
- All triads that share one common tone are grouped together into the term compound transformations (Cohn 1997).
- SLIDE transformations are different than other compound transformations because of the aurally distinct half-step motion in the outer voices (Lewin 1987). The outer voices move up or down by half-steps, causing the audience to hear parallel fifths.
These three types of transformations (basic, compound, and SLIDE) are used to describe the ways a chord can change from one to the next.
Theory and Analysis
Summary of theorem
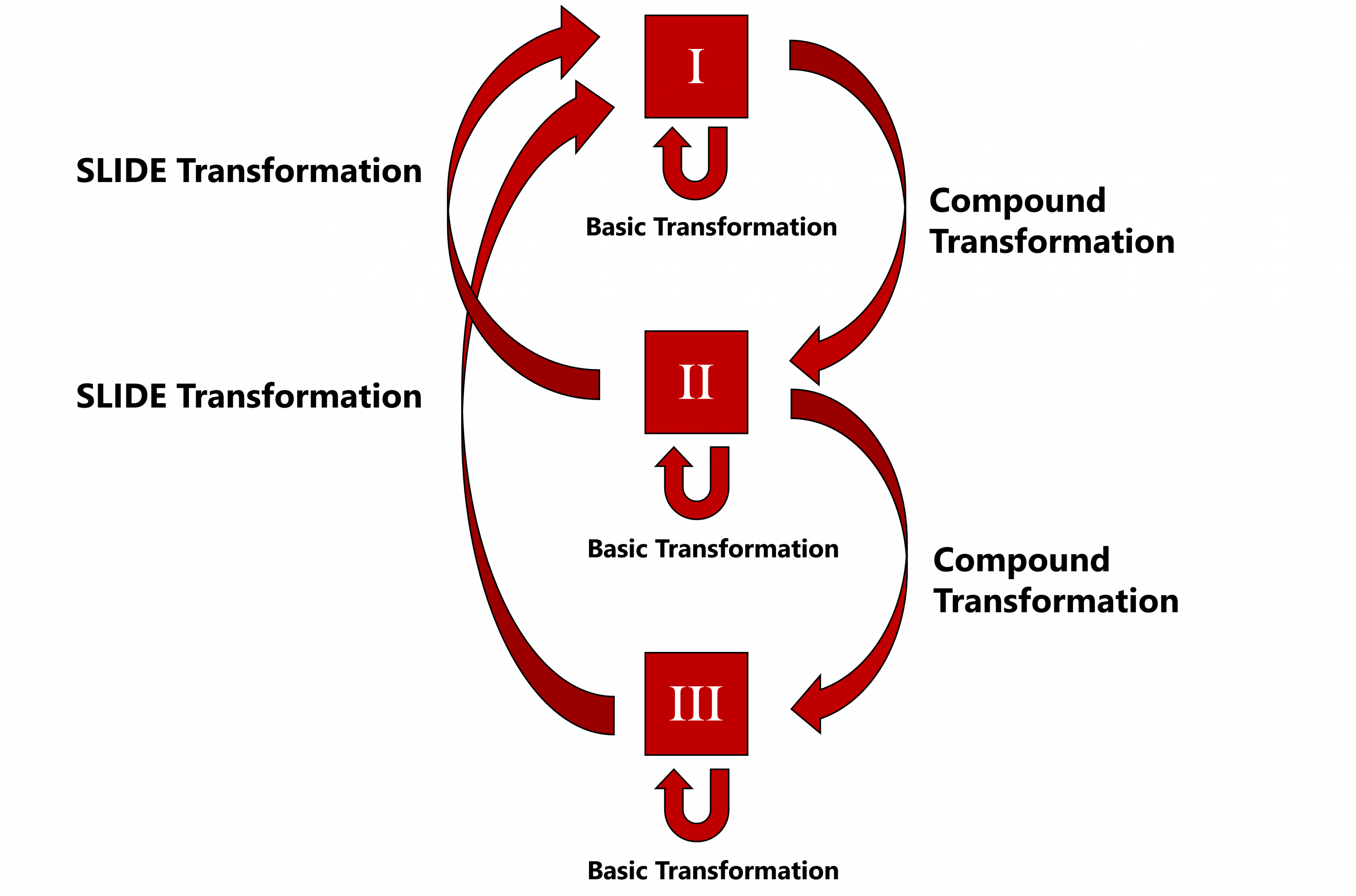
In Figure 1, the roman numerals represent the levels of tension. Level I has no tension, while level II and III have more tension than the previous level. Therefore, phrases always move from level I to level II, sometimes to level III, and always back to level I again. This cycle forms every phrase; multiple cycles form entire sections; and, in larger forms, multiple cycles from the whole piece. Figure 1 also shows how different transformations effect the tension level. When chords undergo transformations (basic, compound, or SLIDE), the tension level stays the same, increases, or is released (level III to level I):
- basic transformations keep the tension level constant.
- compound transformations increases the tension level by one, e.g., a series of chords that are in level I to move to level II.
- SLIDE transformations release tension from level II or III to level I.
Theorem example: “News has a kind of mystery” from Act I, Scene 1 of Nixon in China (m. 347-417)
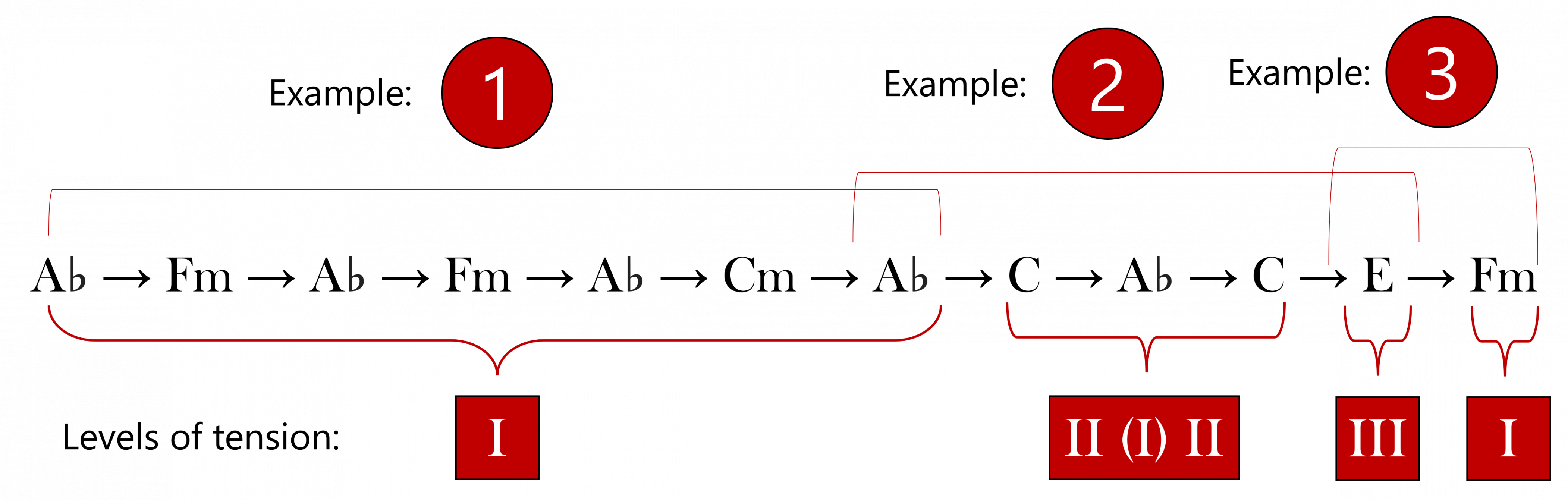
Figure 2 shows a sequence of triads that contains transformational relationships. The levels of tension at the bottom show the movement between the levels of tension, from level I to level III, with a resolution back to level I. From first glance, one can tell that each subsequent chord always shares one note with the chord before it. Where the level remains constant, they share two. In addition, basic transformations always switch modalities, from major to minor and vice versa. In a compound transformation, modality is kept constant, major staying major and minor staying minor. Therefore, there is always a modal contrast between a level increase or a constant progression. Only a SLIDE transformation has a change in modality and a change in level. This is useful when deciphering a previously unseen example and identifying the level changes within it.
See below for further details on each transformation within Figure 2:
- In Example 1 there is no change in tension. The A♭ major chord goes to an F minor chord and vice versa for the first two transformations. These two chords share two common tones, or, using Neo-Riemannian terminology, an R transformation. Then the A♭ major to C minor, an L transformation, occurs but the new chord does not change the tension level as they still share two common tones.
- Example 2 has an increase in tension. From A♭ major to C major (modally similar chords), signals an increase in tension as the two chords sharing only one common tone. The next change, from C major to A♭ major, is a return to level I, not an increase in tension, as it undoes the previous change [1]. The next tensional increase is from C major to E major, as they share just one common tone, E. Now reaching the third level of tension, the tension must be released.
- Example 3 shows the release of tension. From E major to F minor there is a SLIDE transformation. The middle note of E major, G#, is kept constant while the outer voices move up by half-steps. This gives F minor, and a release in tension.
Theorem application to determine form from “News has a kind of mystery” from Act I, Scene 1 of Nixon in China (m. 347 – 509)
A further application of this theory is to determine small scale form. This can be shown in the rest of the aria.
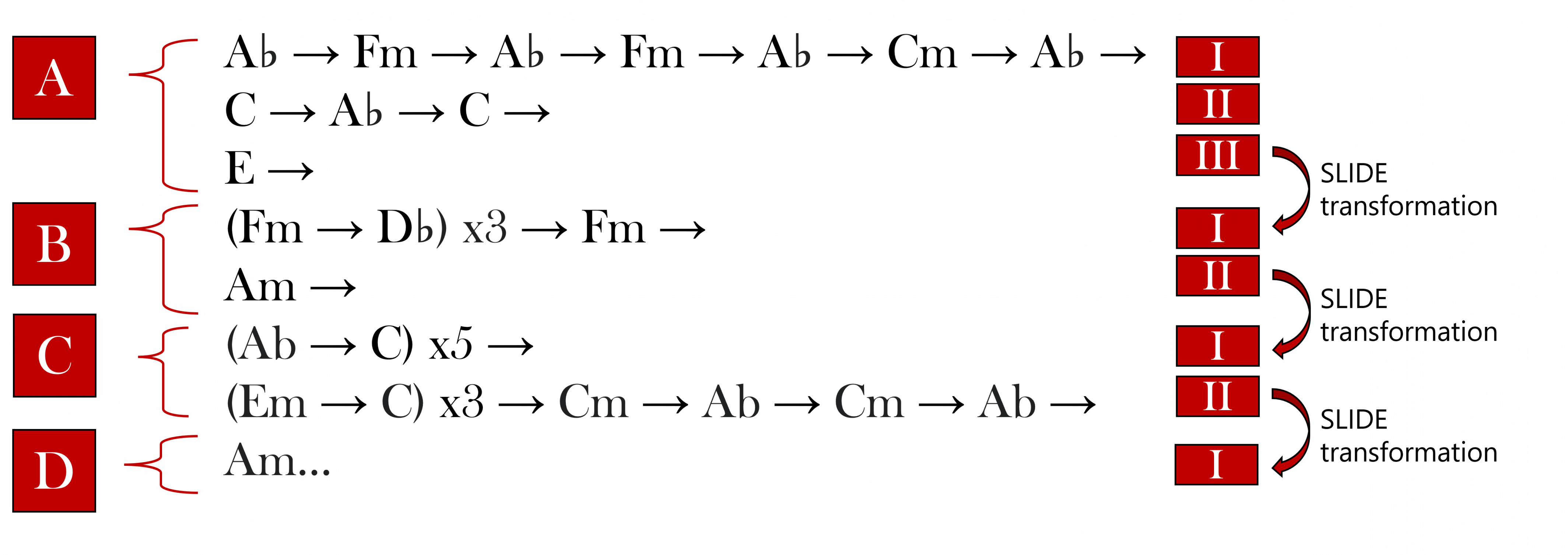
Figure 3 shows the progression of triads in the full first section of the aria “News has a kind of mystery”. Applying level theory, this section can be divided into four sections based on the location of the SLIDE transformations. Each new line indicates a level increase as labeled on the right. Each SLIDE transformation corresponds to a cadential gesture, signaling the ends of sections and phrases. The text of this aria also corresponds to these cadential gestures, with sentences ending at the SLIDE transformations without fail.
This shows the cycles of tension and release in Nixon in China, and one can see that these cycles almost mimic what functional harmony would have achieved in terms of tension and release.
Summary and conclusion
In “News has a kind of mystery” from Nixon in China, we have seen how small form can be derived from the presence of SLIDE transformations, and how those SLIDE transformations are part of a cycle of rising and falling tension. Through the observation of basic and compound transformations, we have seen that phrases go through sections of rising tension and then falling tension through SLIDE transformations. With this framework, we have added tension to transformational harmony—harmony that was traditionally viewed as non-functional and therefore, without the usual tension and release of the tonic, subdominant, and dominant. We have created a quasi-functional system where transformational harmony can go through the same tension and release that functional phrases go through.
Notes
[1] Chords that return to the chord before is quite common in this opera as a whole, and sometimes a loop of three or more chords occur that return to a “home chord”, often cycling though multiple levels. [return to blog]
 Eric Yang is a first-year student studying music theory and vocal performance at the University of Toronto Faculty of Music. He holds diplomas from the London College of Music in Classical Singing and Piano Performance, both at the DipLCM level. As an undergraduate theory student, his interests are in the expansion of transformational harmony, the development of tonal music of modern composers, and computational music analysis. In addition to academic pursuits, Eric has won many accolades in classical voice and currently studies singing with Mark Daboll. In his free time, he enjoys playing trombone, flute, and jazz piano.
Eric Yang is a first-year student studying music theory and vocal performance at the University of Toronto Faculty of Music. He holds diplomas from the London College of Music in Classical Singing and Piano Performance, both at the DipLCM level. As an undergraduate theory student, his interests are in the expansion of transformational harmony, the development of tonal music of modern composers, and computational music analysis. In addition to academic pursuits, Eric has won many accolades in classical voice and currently studies singing with Mark Daboll. In his free time, he enjoys playing trombone, flute, and jazz piano.
Eric recently won second place in the Faculty of Music Undergraduate Research Showcase (FOMURS 2022) for his poster entitled "Tension and Transformational Harmony : Arias from John Adams's Nixon in China (1987)" (see his poster).
Eric also received a Patricia and Peter Shannon Wilson Undergrad Research Prize (2022) for his research.
References
Adams, John. 1994. Nixon In China. London: Boosey & Hawkes.
———. 2008. Hallelujah Junction. New York: Farrar, Straus and Giroux.
Capuzzo, Guy Capuzzo. 2004. “Neo-Riemannian Theory and the Analysis of Pop-Rock Music.” Music Theory Spectrum 26, no. 2: 177–200. https://doi.org/10.1525/mts.2004.26.2.177.
Childs, Adrian P. 1998. “Moving beyond Neo-Riemannian Triads: Exploring a Transformational Model for Seventh Chords.” Journal of Music Theory 42, no. 2: 181–93. https://doi.org/10.2307/843872.
Cohn, Richard. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15, no. 1: 9–40. https://doi.org/10.2307/854168.
———.1997. “Neo-Riemannian Operations, Parsimonious Trichords, and Their ‘Tonnetz’ Representations.” Journal of Music Theory 41, no. 1: 1–66. https://doi.org/10.2307/843761.
———. 1998. “Introduction to Neo-Riemannian Theory: A Survey and a Historical Perspective.” Journal of Music Theory 42, no. 2: 167–80. https://doi.org/10.2307/843871.
Hook, Julian. 2007. “Cross-Type Transformations and the Path Consistency Condition.” Music Theory Spectrum 29, no. 1: 1–40. https://doi.org/10.1525/mts.2007.29.1.1.
Johnson, Timothy. 2011. John Adams’s Nixon in China: Music Analysis, Historical and Political Perspectives. Surrey: Ashgate Publishing.
Lehman, Frank. 2014. “Schubert’s SLIDEs: Tonal (Non-)Integration of a Paradoxical Transformation”. Music Theory and Analysis (MTA) 1, no 1–2: 61–100. https://doi.org/10.11116/MTA.1.4.
Lewin, David. 1987. Generalized Musical Intervals and Transformations. New York: Oxford University Press. Oxford Scholarship Online. https://doi.org/10.1093/acprof:oso/9780195317138.001.0001.
Lord, Winston. 2004. “Mao Zedong Meets Richard Nixon, February 21, 1972.” USC US-China Institute. https://china.usc.edu/mao-zedong-meets-richard-nixon-february-21-1972.
May, Thomas. 2006. “John Adams Reflects on His Career.” The John Adams Reader: Essential Writings on an American Composer, edited by Thomas May. Pompton Plains: Amadeus Press.
Schwartz, David. 1992. “Postmodernism, the Subject, and the Real in John Adams’s Nixon in China.” Indiana Theory Review 13, no. 2: 112. http://www.jstor.org/stable/24046021
Warburton, Dan. 1988. “A Working Terminology for Minimal Music.” Intégral 2: 135–59. http://www.jstor.org/stable/40213909.